Introducción a las Progresiones y Series Aritméticas NM/NS
Por Romina Biga, Susana Beatriz Fernández, Marcos Guerrero, Silvia Cano, Alexander Díaz Campos, Miriam Bertone, Guillermo Rodriguez, Maria Ines Piaggio, Montse Martí, Elisa Jimenez Grant, Katherine Guerrero, María Gabriela Salatino, Germán Tenorio, Rafaela Menoscal, Sol Ines Perez, Pedro Martínez Marecos, Cecilia Villavicencio, Francisco Vargas Fragosa., Barbara Battaglino, Karina Avendanño, Tulia Ocampo Gaviria, Leonor Alvarez, Marcela Scarone, David Spooner, Analía Oursi, Maite de la Fuente Zofío, Eugenio López Braos, Prof. Alfonso Perendones, Cristina Flammini, Eugenia Arias, Prof. Jesús Montoro Ruiz, José Enrique García Cebrián
Progresiones o Secuencias Aritméticas
Dada la siguiente secuencia de imágenes ¿cuál crees que será el número de palillos que se requieren en el diagrama número 58? ¿cuántos palillos en total necesitaremos para realizar los primeros 58 diagramas?
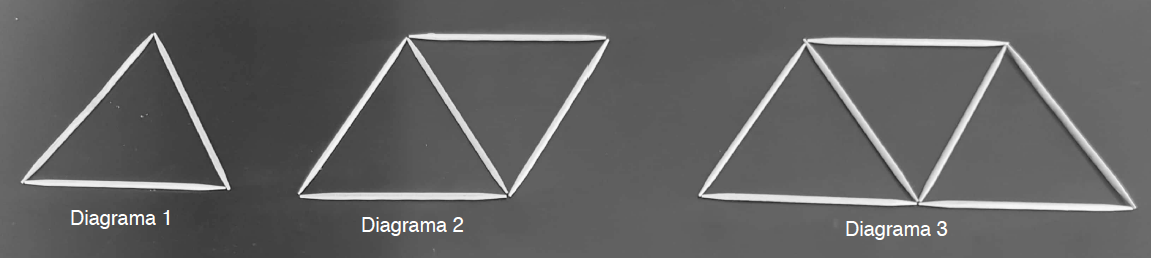
Es posible hallar el patrón detrás de esta secuencia de la siguiente forma. Representaremos los términos de la secuencia como:
Al restar dos términos consecutivos se obtiene la misma diferencia. Tal número se denomina la diferencia común y se representa con la letra 
Así: 
Cuando en una secuencia tenemos una diferencia común entre cualesquiera par de términos consecutivos se denomina Progresión o Secuencia Aritmética.
Para obtener el segundo término de la secuencia debemos sumar la diferencia común al primer término una vez, para obtener el tercer término se suma la diferencia común al primer término dos veces, y así sucesivamente, es posible obtener el número de palillos que contendrá el diagrama 58:
El término enésimo de una Progresión o Secuencia Aritmética es: 
. Donde 
representa la posición del término, 
el primer término y 
la diferencia común de dos términos consecutivos en la progresión. En general: 
Ahora bien, al sumar los primeros 
términos de una progresión aritmética "Serie Aritmética" se tiene que:
En resumen tenemos que en cualquier Progresión o Secuencia Aritmética:
Término enésimo: 
La suma de los primeros términos "Serie Aritmética": 
Así pues, el número total de palillos que necesitaremos para realizar los primeros 58 diagramas será:
Luego, se requieren 3 480 palillos en total para realizar los primeros 58 diagramas.
A continuación se adjunta una guía de trabajo relacionada con Progresiones Aritméticas.